Most of the remaining parts of the first chapter of NLTK book serve as an introduction to Python in the context of text processing. I won't translate that to Lisp, because there're much better resources explaining how to use Lisp properly. First and foremost I'd refer anyone interested to the appropriate chapters of Practical Common Lisp:
It's only worth noting that Lisp has a different notion of lists, than Python. Lisp's lists are linked lists, while Python's are essentially vectors. Lisp also has vectors as a separate data-structure, and it also has multidimensional arrays (something Python mostly lacks). And the set of Lisp's list operations is somewhat different from Python's. List is the default sequence data-structure, but you should understand its limitations and know, when to switch to vectors (when you will have a lot of elements and often access them at random). Also Lisp doesn't provide Python-style syntactic sugar for slicing and dicing lists, although all the operations are there in the form of functions. The only thing which isn't easily reproducible in Lisp is assigning to a slice:
>>> sent[1:9] = ['Second', 'Third']
>>> sent
['First', 'Second', 'Third', 'Last']There's replace but it can't shrink a sequence:
CL-USER> (defvar sent '(1 2 3 4 5 6 7 8 9 0))
CL-USER> (replace sent '("Second" "Third") :start1 1 :end1 9)
(1 "Second" "Third" 4 5 6 7 8 9 0)Ngrams
So, the only part worth discussing here is statistics.
Let's start with a frequency distribution. We have already used something similar in the previous part for text generation, but it was very basic and tailored to the task. Now, it's time to get into some serious language modeling and discuss a more general-purpose implementation.
Such modeling is accomplished via collecting of large amounts of statistical data about words and their sequences appearances in texts. These sequences are called ngrams. In a nutshell, you can think of ngrams distribution as a table mapping ngram sequences to numbers.
(defclass ngrams ()
((order :initarg :order :reader ngrams-order)
(count :reader ngrams-count)
(max-freq :reader ngrams-max-freq)
(min-freq :reader ngrams-min-freq)
(total-freq :reader ngrams-total-freq)))The crucial parameter of this class is order which defines the
length of a sequence. In practice, ngrams of order from 1 to 5 may be
used.
ngrams is an abstract class. In Lisp you don't have to somehow
specify this property, you just don't implement methods for it. The
simplest ngrams implementation — table-ngrams — uses an in-memory
hash-table as a store. You can get ngram frequency and "probability"
(the maximum likelihood estimation) from it, as well as log of
probability which is used more often in calculations, because it
allows to avoid the problem of floating point rounding errors
occurring when multiplying probabilities which are rather small
values.
NLTK> (freq (text-bigrams *moby*) "The whale")
Indexing bigrams...
Number of bigrams: 116727
14
NLTK> (logprob (text-bigrams *moby*) "The whale")
-14.255587So how do we get bigrams of Moby Dick? For that we just have to count all of them in text (this is a simplified version — some additional processing for sentence start/ends is needed):
(defun index-ngrams (order words &key ignore-case)
(make 'table-ngrams :order order
:table
(let ((ht (make-hash-table :test (if ignore-case 'equalp 'equal))))
(do ((tail words (rest tail)))
((shorter? tail order))
(incf (get# (if (= order 1)
(car tail)
(sub tail 0 order))
ht 0)))
ht)))table-ngrams will be useful for simple experimentation and prototyping,
like we do in our NLTK examples.
NLTK> (defvar *1grams* (text-ugrams *moby*))
Indexing unigrams...
Number of unigrams: 1924
NLTK> (freq *1grams* "whale")
906
NLTK> (take 50 (vocab *1grams* :order-by '>))
("," "the" "<S>" "</S>" "." "of" "and" "-" "a" "to" ";" "in" "\"" "that" "'"
"his" "it" "I" "!" "s" "is" "he" "with" "was" "as" "all" "for" "this" "at"
"by" "but" "not" "him" "from" "be" "on" "?" "so" "whale" "one" "you" "had"
"have" "there" "But" "or" "were" "now" "which" "me")The strings "<S>" and "</S>" here denote special symbols for sentence
start and end.
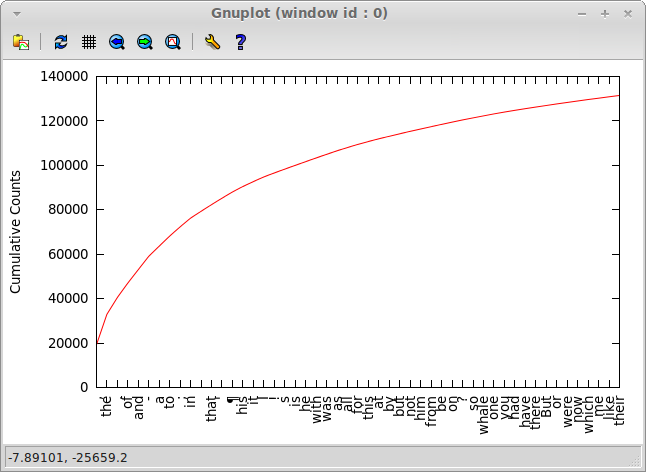
Here's a cumulative plot of them:
And here's just the counts graph:
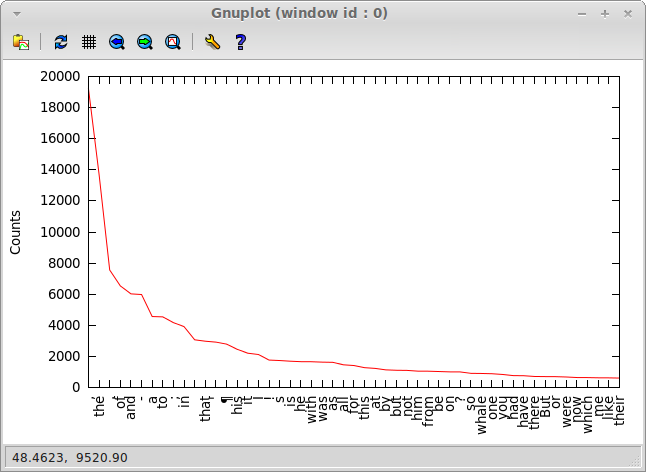
And, finally, here's hapaxes:
NLTK> (take 50 (hapaxes (text-ugrams *moby*)))
("orphan" "retracing" "sheathed" "padlocks" "dirgelike" "Buoyed" "liberated"
"Till" "Ixion" "closing" "suction" "halfspent" "THEE" "ESCAPED" "ONLY"
"Epilogue" "thrill" "etherial" "intercept" "incommoding" "tauntingly"
"backwardly" "coincidings" "ironical" "intermixingly" "whelmings" "inanimate"
"animate" "lookouts" "infatuation" "Morgana" "Fata" "gaseous" "mediums"
"bewildering" "bowstring" "mutes" "voicelessly" "THUS" "grapple"
"unconquering" "comber" "foregone" "bullied" "uncracked" "unsurrendered"
"Diving" "flume" "dislodged" "buttress")The next Python feature showcased here is list comprehensions.
The idea behind them is to resemble theoretical-set notation in list
definition. There's no such thing out-of-the box in Lisp (although you
can implement an even closer to set-notation variant in
just 24 lines),
and the general approach is to favor functional style filtering with
variants of map and remove-if.
NLTK> (sort (remove-if #`(< (length %) 15)
(uniq (text-words *moby*)))
'string<)
("CIRCUMNAVIGATION" "Physiognomically" "apprehensiveness" "cannibalistically" "characteristically" "circumnavigating" "circumnavigation" "circumnavigations" "comprehensiveness" "hermaphroditical" "indiscriminately" "indispensableness" "irresistibleness" "physiognomically" "preternaturalness" "responsibilities" "simultaneousness" "subterraneousness" "supernaturalness" "superstitiousness" "uncomfortableness" "uncompromisedness" "undiscriminating" "uninterpenetratingly")
NLTK> (sort (remove-if #`(or (<= (length %) 7)
(<= (freq (text-ugrams *chat*) %) 7))
(vocab (text-ugrams *chat*)))
'string<)
("20sUser104" <... another 130 users ...> "Question" "actually" "anything" "computer" "everyone" "football" "innocent" "listening" "remember" "seriously" "something" "talkcity_adults" "thinking" "together" "watching")In NLTK variant all users are removed from the corpus with some pre-processing.
Language Modeling
But to be useful for real-world scenarios ngrams have to be large, really large (on the orders of tens of gigabytes of data for trigrams). This means that you won't be able to simply store them in memory and will have to use some external storage: a general-purpose data-store, like the relational database or a special-purpose software.
One such ngrams service that is available on the internet is
Microsoft Web N-gram Services.
If you have a developer token you can query it over HTTP. The service
only returns log-probabilities and also log-conditional-probabilities
and runs really slow, but it is capable of serving batch requests,
i.e. return probabilities for several ngrams at once. The
implementation of ngrams interface for such service is provided in
contrib/ms-ngrams.lisp.
We have already encountered conditional probabilities in the previous part. They have the following relationship with regular (so called, "joint") probabilities (for bigrams):
p(A,B) = p(B|A) * p(A)
where P(A,B) is a joint probability and P(B|A) is the conditional oneI.e. they can be calculated from current ngrams plus the ngrams of
preceding order. So, this operation is performed not on a single
ngrams object, but on a pair of such objects. And they serve an
important role we'll see below. But first we need to talk about
language models.
A language model is, basically, a collection of ngrams of different orders. Combining these ngrams we're able to obtain some other measures beyond a simple frequency value or probability estimate. The biggest added value of such model is in smoothing capabilities that it implements. The problem smoothing solves is that you'll almost never be able to have all possible ngrams in your data-store — there's just too many of them and the language users keep adding more. But it's very nasty to get 0 probability for some ngram. The language model allows to find a balance between the number of ngrams you have to store and the possibility to get meaningful probability numbers for any ngram. This is achieved with various smoothing techniques: interpolation and discounting. Some of the smoothing methods are:
- +1 smoothing
- Kneser-Ney smoothing
- and Stupid backoff
A good general compilation of various smoothing methods is assembled in this presentation.
Let's look at the simplified implementation of scoring a sentence with the Stupid Backoff model:
(defmethod logprob ((model language-model) (sentence list))
(with-slots (order) model
(let ((rez 0)
(s (append (cons "<S>" sentence) (list "</S>"))))
(when (shorter? s order)
(return-from logprob (logprob (get-ngrams (length s) model) s)))
;; start of the sentence: p(A|<S>) * p(B|<S>,A) * ...
(do ((i 2 (1+ i)))
((= i order))
(incf rez (cond-logprob model (sub s 0 i))))
;; middle of the sentence
(do ((tail s (rest tail)))
((shorter? tail order))
(incf rez (cond-logprob model (sub tail 0 order))))
rez)))Eventually, the language model is able to return the estimated probability of any sequence of words, not limited to the maximum order of ngram in it. This is usually calculated using the Markov assumption with the following formula (for a bigram language model):
p(s) = p(A) * p(B|A) * p(C|A,B) * p(D|B,C) * ... * p(Z|X,Y)
where s = A B ... Z
NLTK> (defvar *moby-lm2* (make-lm 'stupid-backoff-lm
:1g (text-ugrams *moby*)
:2g (text-bigrams *moby*)))
NLTK> (prob *moby-lm2* "This is a test sentence.")
6.139835e-20That was, by the way, the probability of an unseen sentence with the word "sentence" completely missing from vocabulary.
NLTK> (prob *moby-lm2* '("<S>" "Moby" "Dick" "." "</S>"))
5.084481e-9
NLTK> (float (prob (text-bigrams *moby*) '("Moby" "Dick")))
3.0310333e-4As you see, it's much more likely to encounter the sentence "Moby Dick." in this text, although not so likely as the phrase "Moby Dick". :)
Also such model is able to generate random texts just like we did in
the previous part. But because of the smoothing capability it's much
more general, i.e. it can generate sequences with any word from the
vocabulary, even the phrases unseen before. At the same time it's much
more computationally expensive, because now generating each new word
takes O(vocabulary size) while it was O(average number of words
following any particular word).
NLTK> (princ (generate *genesis* :order 2 :n 93))
burial to judged eaten sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung sprung foreign longed them ought up Temanites Aran earth earth blessings surface surface surface surface surface surface surface surface surface floated Darkness Now homage earth Now In princes said vengeance It passed said divide In beginning earth Asenath said re The peaceful kind Calah said blameless mistress Chaldees said hunter said middle surface surface surface surface yonder earth rib said said smoking smoking smokingAnd, as you see, this example totally doesn't resemble the one in the previous part. Is this a bug? No, just a trick that is played with us because we aren't following the basic math principles. In the Stupid Backoff model the probabilities don't add up to 1 and the conditional probability of an unseen ngrams may be larger than the largest probability of any recorded one! This is the reason we get to produce sequences of repeated words. This problem is much less obvious for the trigram model, although the text remains a complete gibberish.
NLTK> (princ (generate *genesis* :order 3 :n 93))
brink time wagons fourth Besides south darkness listen foreigner Stay possessor lentils backwards be call dignity Kenizzites tar witness strained Yes appear colts bodies Reuel burn inheritance Galeed Hadar money touches conceal mighty foreigner spices Set pit straw son hurry yoke numbered gutters Dedan honest drove Magdiel Nod life assembly your Massa iniquity Tola still fifteen ascending wilderness everywhere shepherd harm bore Elah Jebusites Assyria butler Euphrates sinners gave Nephilim Stay garments find lifted communing closed Ir lights doing weeping shortly disobedience possessions drank peoples fifteen bless talked songs lamb far Shaveh heavensWhat this example shows us are at least two things:
- we should always check that mathematical properties of our models still hold as we tweak them
- although the major use-case for language model is scoring, you can get a feel of how good it will perform by looking at the texts it generates
Finding collocations
This is another interesting and useful NLP problem with a very elegant baseline solution, which is explained in this article. Hopefully, we'll get back to it in more detail in the future chapters. And for now here's the results of implementing the algorithm from the article:
NLTK> (collocations *inaugural*)
(("United" "States") ("fellow" "citizens") ("four" "years") ("years" "ago")
("Federal" "Government") ("General" "Government") ("American" "people")
("Vice" "President") ("Old" "World") ("Almighty" "God") ("Fellow" "citizens")
("Chief" "Magistrate") ("Chief" "Justice") ("God" "bless") ("go" "forward")
("every" "citizen") ("Indian" "tribes") ("public" "debt") ("one" "another")
("foreign" "nations") ("political" "parties") ("State" "governments")
("National" "Government") ("United" "Nations") ("public" "money")
("national" "life") ("beloved" "country") ("upon" "us") ("fellow" "Americans")
("Western" "Hemisphere"))I'm surprised at how similar they are to NLTK's considering that I didn't look at their implementation. In fact, they are the same up to the difference in the list of stopwords (the dirty secret of every NLP application :) The code for collocation extraction function can be found in core/measures.lisp.
Other uses of ngrams
Ngrams are also sometimes used for individual characters to build Character language models. And here's another usage from NLTK — for counting word lengths.
NLTK> (defvar *moby-lengths*
(index-ngrams 1 (mapcar #'length (text-words *moby*))))
NLTK> (vocab *moby-lengths*)
(1 4 2 6 8 9 11 5 7 3 10 12 13 14 16 15 17 18 20)
NLTK> (ngrams-pairs *moby-lengths*)
((1 . 58368) (4 . 42273) (2 . 35726) (6 . 17111) (8 . 9966) (9 . 6428)
(11 . 1873) (5 . 26595) (7 . 14399) (3 . 49633) (10 . 3528) (12 . 1053)
(13 . 567) (14 . 177) (16 . 22) (15 . 70) (17 . 12) (18 . 1) (20 . 1))
NLTK> (ngrams-max-freq *moby-lengths*)
58368
NLTK> (freq *moby-lengths* 3)
49633Final thoughts
Language modeling is really the foundation of any serious NLP work. Having access to ngrams expands your possibilities immensely, but the problem with them is that moving from prototype to production implementation becomes tricky due to the problems of collecting a representative data-set and consequently efficiently storing it. Yet, there are solutions: the Google Books Ngrams and Google Web1T are an example of web-scale ngrams data-set, and there's also special-purpose software for storing large ngrams corpora and obtaining language models from them. The notable examples are BerkeleyLM and KenLM.
Here's a link to some code for this chapter.- Previous: NLTK 1.1 - Computing with Language: Texts and Words


No comments:
Post a Comment